Implementing kernalized regression from scratch in python

Mar 10, 2021

Originally published on medium.com on 10. March 2021.

Okay, there are already plenty of articles describing linear regression but I have not seen much on kernelized regression. Well the fact that you are reading this means that you also didn’t find what you were looking for…

For completeness we will get started with ordinary linear regression.

Ordinary Linear Regression

First we need some data that we can play with. Here we will just create some arbitrary 2 dimensional samples.

import numpy as np
import matplotlib.pyplot as plt

x=np.linspace(2,30,100)
y= 2*(x+15)+np.random.random_sample(x.shape)*5+2
x=x[:,np.newaxis]
show(x,y)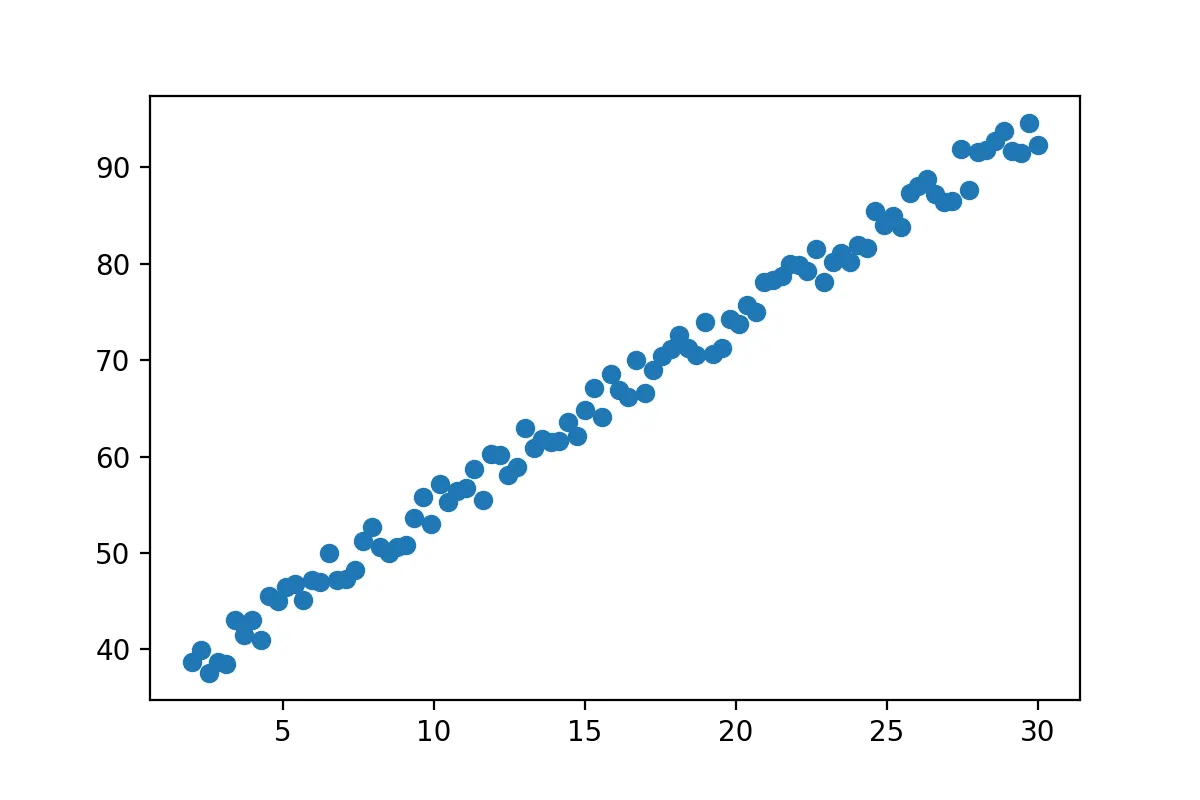

You can think of this data as whatever you want. Here we can clearly see that there is a strong correlation between the two variables. The x-axis could be price of a bus-ticket and y-axis could be the distance traveled, as we would expect a strong correlation there. Youre data likely looks completely different but linear regression works all the same.

Let’s have a closer look at the data. In our case the data X is just one dimensional but we will take multiple samples so we have n=100 samples each of dimension d=1.

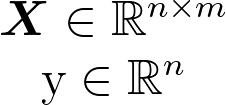
We know the equation of a line is y=mx. We simply let our data X represent the general x and then we just need to solve for m.

Since we can not invert a matrix that isn’t square we simply make X square by multiplying with its own transpose before inversion. To get the original shape back and by magic of math we multiply by the transpose again and get what’s know as Moore–Penrose inverse.

Okay finally time for more code.

k = np.linalg.inv(np.dot(x.T,x))
m=np.dot(k,np.dot(x.T,y))
show(x,y,0,m)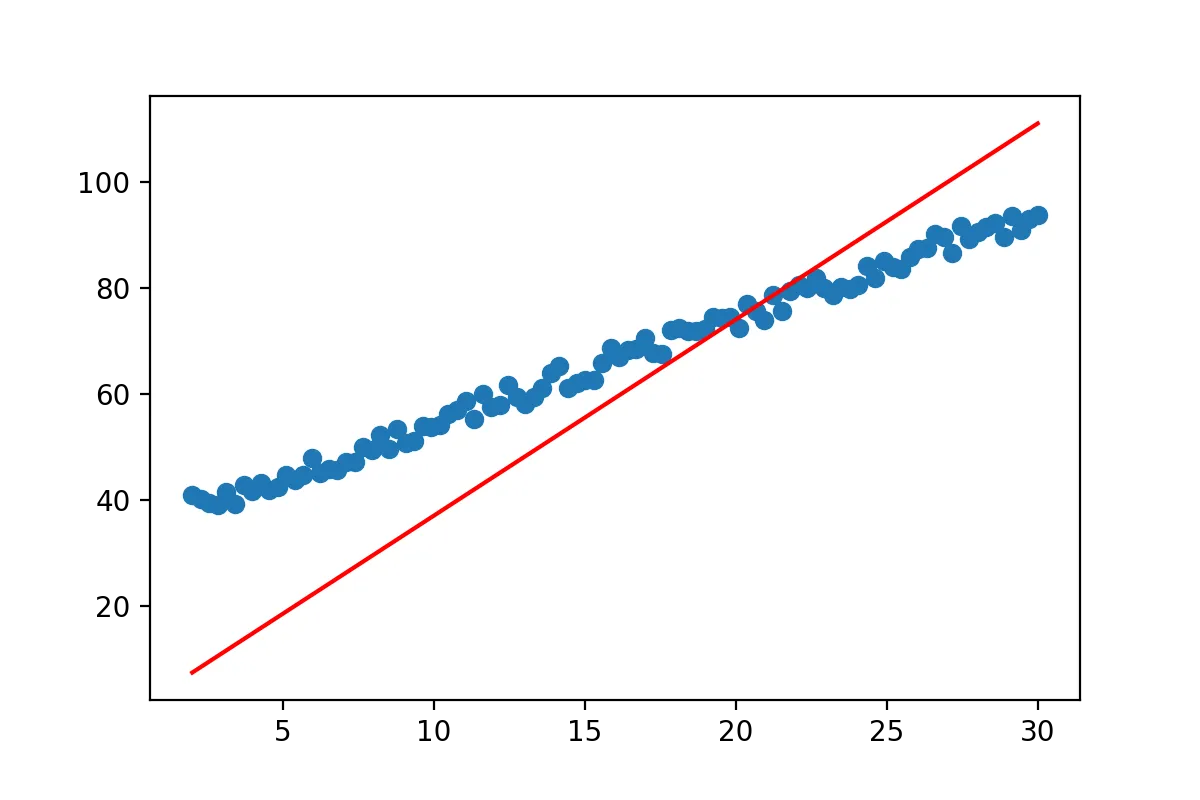

Well we got a line… but it doesn’t really match the data yet. So what went wrong? The line equation that we started with y=mx will always pass through (0,0). No matter what value you pick for m at x=0, y has to be 0. However the regression line we expect from our data does not pass through (0,0). So we have to adjust our line equation so that it’s y-value at x=0 can be fitted by our approach. We all know from school that we can simply add a constant to our line formula to end up with y=mx+b.

How are we going to this with our current equation? Let’s look at what we have so far: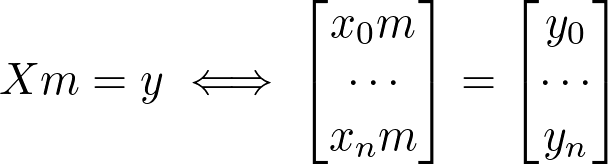

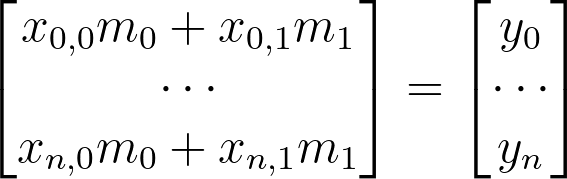
Now if we just add an extra dimension to our data we can notice that the same multiplication of X and m will require m to be 2 dimensional as well. And the matrix multiplication looks like this:

Now if we set x[:,1]=1 and we view m[1] as b we get the line equation with our bias b! So we don’t even need to change our equation at all!

x=np.stack([x[:,0],np.ones(x.shape[0])],axis=1).reshape(-1,2)
k = np.linalg.inv(np.dot(x.T,x))
m=np.dot(k,np.dot(x.T,y))
show(x[:,0],y,m[1],m[0])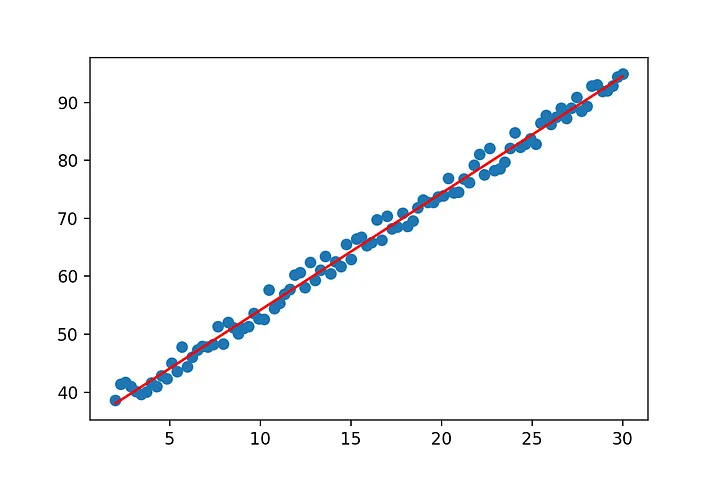

That looks much better already!

We are not going to discuss the remaining topics in detail. The rest is just to get you started and give you a general idea.

Ridge Regression

Sometimes the pseudo-inverse can run into trouble which can be avoided if we add a small value to our matrix before computing the inverse. This is known as ridge regression.

small_arbitrary_value=0.1
k = np.linalg.inv(np.dot(x.T,x)+small_arbitrary_value*np.eye(x.shape[1]))
m=np.dot(k,np.dot(x.T,y))
show(x[:,0],y,m[1],m[0])

Primal vs Dual Form

So far we have been implementing the primal form. If we look at the dimensions we notice that the matrix that we have to inverse is a square matrix of the dimension 2. Just like our (extended) samples in X.

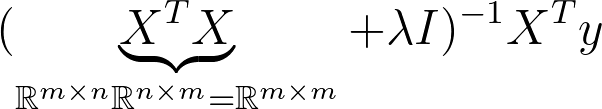
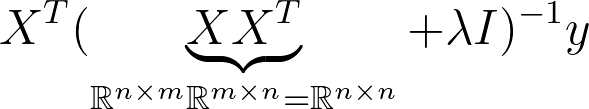
However, we can compute the inverse just as well by changing the order of the transpose.

This is known as the dual Form. Notice that the matrix that needs to be inverted is know a square matrix of the dimension n x n. This is much more expensive to compute when we have more samples than dimensions in X. So most of the time we want to avoid this. However it can be useful to derive solutions for classification problems such as SVM so it’s good to have seen this before.

Kernel Regression

We now know how to compute a linear regression. But often data is not linear … we could come up with non linear regression methods. But we just picked up linear regression so let’s see what we can do. If we add a few dimensions to our input data we might be able to a linear regression in the higher dimension(feature space). Or a linear separation as depicted below:

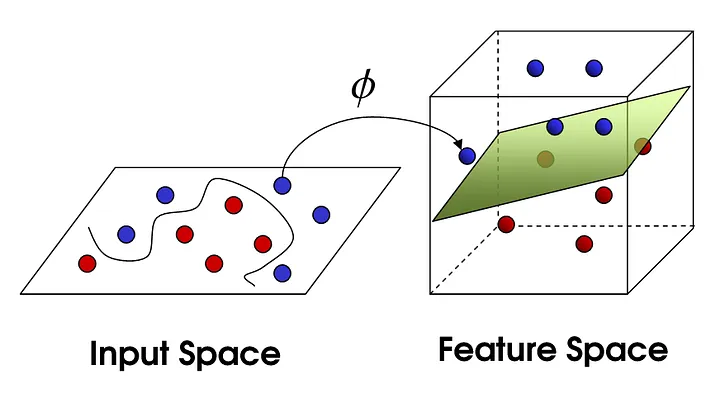
CC BY-SA 4.0Photo by Shehzadex on Wikimedia

What does that transformation look like? Just to give you an idea a simple polynomial mapping could look like this: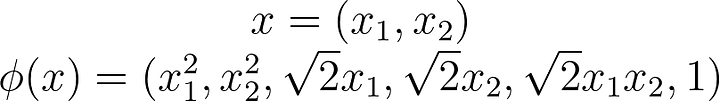

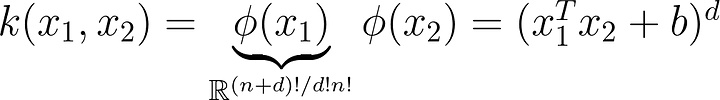
Well that certainly look like a lot of work for us and the computer. We went from 2 dimension to 6. Not only do we have to compute that embedding in the first place, anything we do from here on has to work on the 6 dimensions rather than 2. Luckily some smart people noticed that there are certain special transformation where we can reduce a dot product in the feature space, thats the new high dimensional space, to a simple evaluation in the original dimension low dimensional space!

Though it might not look like much.This is HUGE. So for example the polynomial function is such a special kernel function (Mercer Kernel). For a simply polynomial kernel the feature map already has a ridiculously large dimension:

We can replace any vector dot-product of this behemoth with a simply function. Even better looking at our linear regression we notice that our data X occurs only in dot-product so we can replace all of them!

def kernel(x_i,x_j):
    #return np.dot(x_j,x_i) # Linear Kernel, same as not using Kernels at all
    #return np.dot(x_j,x_i)**2 # Polynomial Kernel
    return np.exp(-0.5*np.linalg.norm(x_i-x_j)) # Gaussian Kernel


# let's set up some non linear data
y= np.sin(x[:,0])+x[:,1]
y= x[:,0] + 4*np.sin(x[:,0])+ 4*np.random.rand(x.shape[0])

# We could just call the kernel function every time
# Instead we store the solutions in this matrix
# to save some computations
K=np.zeros((x.shape[0],x.shape[0]))
for i, row in enumerate(K):
    for j, col in enumerate(K.T):
        K[i,j]=kernel(x[i,:],x[j,:])

You can find a few more kernel functions here.

Now we just take our by now familiar linear regression and replace all dot products with kernel functions.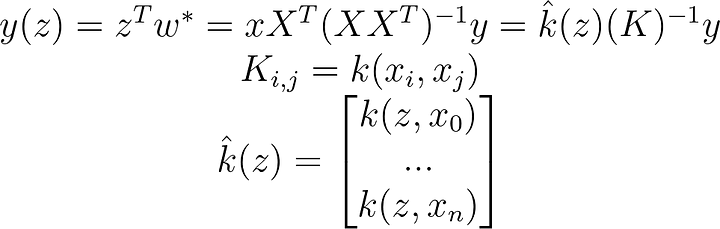

Notice that we also have to embed the vector at which we evaluate the regression, here z. Putting this into code we get:

a = np.linalg.inv(K+0.1*np.eye(K.shape[0]))
m=np.dot(y,a)

x_pred=np.arange(0,35,0.2)
x_pred=np.stack([x_pred,np.ones(x_pred.shape[0])],axis=1).reshape(-1,2)
y_pred=np.zeros(x_pred.shape[0])
for outer_i, x_p in enumerate(x_pred):
    k = np.zeros(x.shape[0])
    for i, row in enumerate(k):
        k[i]=kernel(x_p,x[i,:])
    y_pred[outer_i]=np.dot(m,k)

show(x[:,0],y,x_2=x_pred[:,0],y_2=y_pred)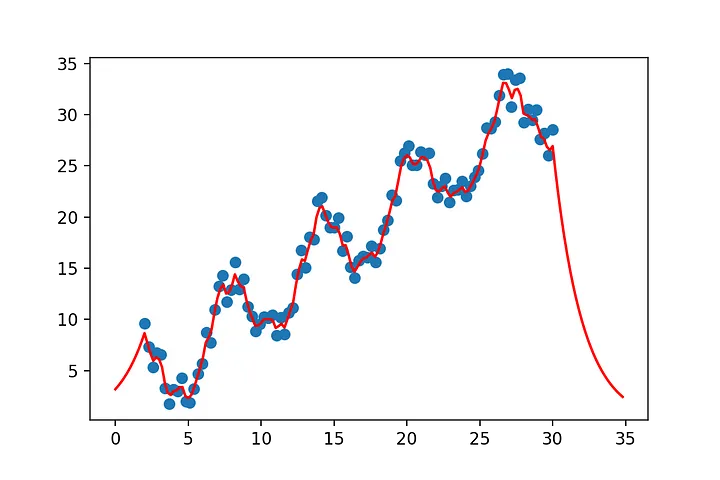

A nice non-linear regression using the kernel trick! For completeness here is the code used for the graphs:

def show(x_sample,y,a=0,b=0, x_2=None,y_2=None):
    if b !=0:
        plt.plot(x_sample,a+b*x_sample , c='red')

    if x_2 is not None:
        plt.plot(x_2,y_2, c='red')
    plt.scatter(x_sample, y)
    plt.show()