Fast ray-AABB Intersection test
As suggested by Excercise 9 in Chpater 4 I replaced the original ray-AABB (Axis Aligned Bounding Box) collision with the algorithm proposed by Martin Eisemann et. al 2007.
General Idea
In order to hit a 2D AABB the ray has to pass through it’s diagonal. What diagonal to consider depends on the direction of the ray. Each component of the direction vector is either Zero (O), Positive (P) or Negative (M), thus each ray can be categorized as a combination of $(x,y,z) : x,y,z \in {O,P,M} $. For each type we can derive what diagonal the ray has to pass through in order to hit the box. This diagonal is confined by the vectors $ a,b $, in order to pass through the diagonal, the slope of the ray has to be greater than the slope of $ a $ and less than the slope of $ b $. The slope is defined as $ S_{xy} = {d_x}/{d_y} $. Or if we reverse the logic the ray misses if the folling is true:
$$ S_{xy}( r(t) ) > S_{xy}( b(t) ) \lor S_{xy}( r(t) ) < S_{xy}( a(t)) $$
As can be observed in the figures below the diagonal and thus $ a,b $ depend on the orientation thus the type of the ray. In 3D we need to consider 3 faces of each box thus 26 possible types must be implemented individually. (There are 26 types since we ignore the degenerate case of (O,O,O) leaving us with $ (3³ -1) $ types).
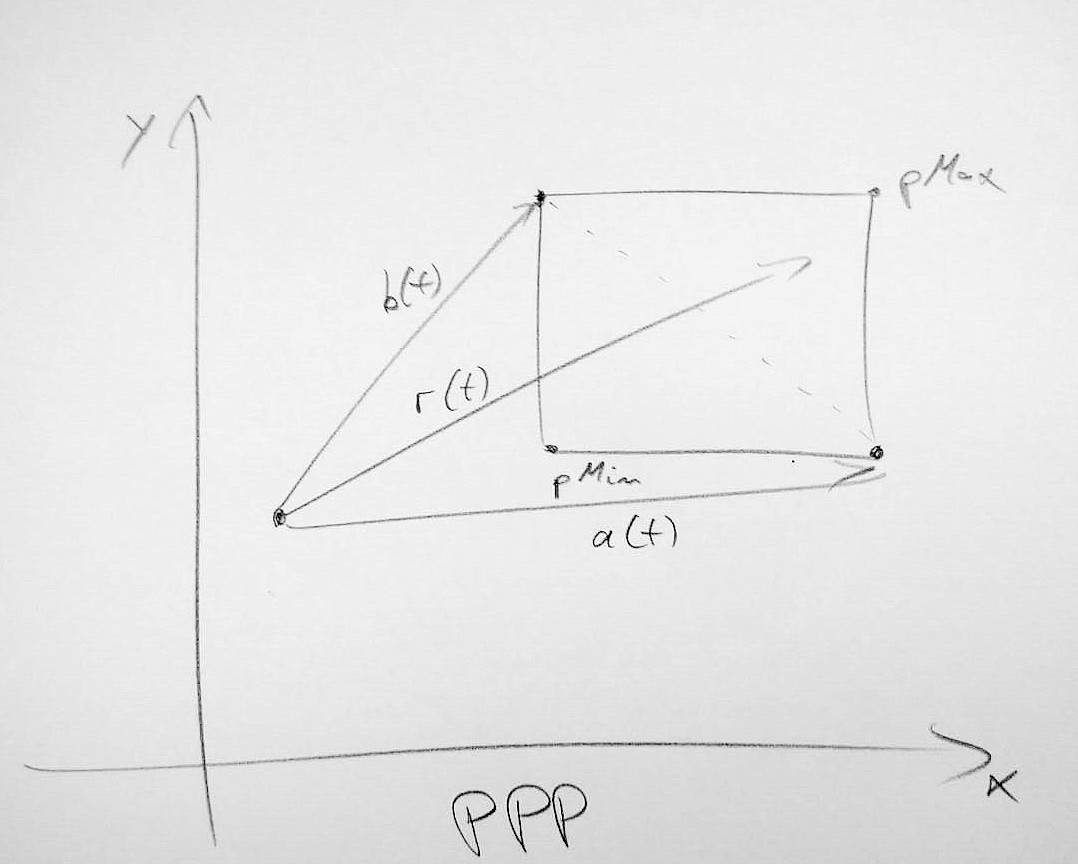
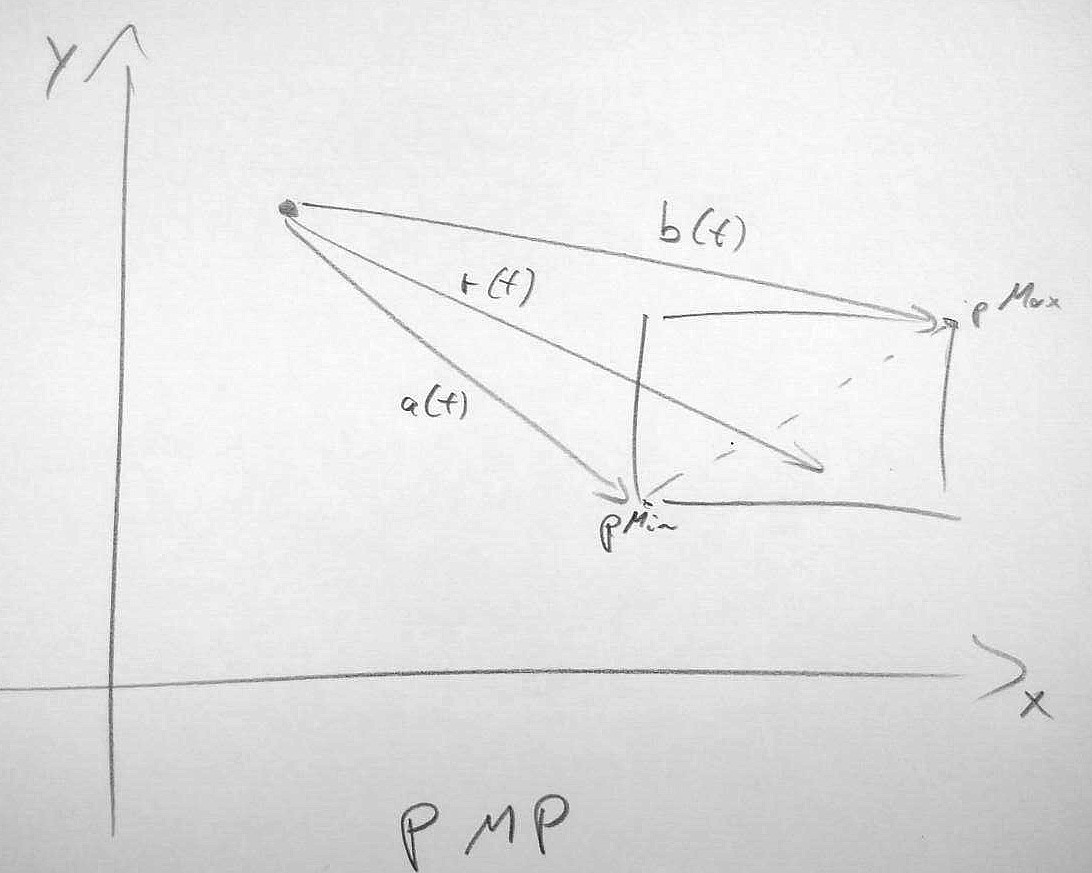
As most values needed can be precomputed this approach is in theory faster as other intersection-tests. For a more complete description please consult the original paper.
Implementation
The inverse direction ($id$), slope-values ($S_{..}$) as well as the precomputed values $ C_{..} $ need to be stored in the Ray-Object. However we still need to store the type of the ray and when it comes to the intersection test we need to be able to call the correct implementation. Two possible implementations came to mind:
- The use a enum to encode the type and then implement a large switch-case in the boundingBox intersect method. However this leads to a very long intersection-method that is very hard to navigate. Also this introduces further branching in the intersection function.
- The use of function pointer which point to the correct implementation for this ray. While this does improve readability it prevents the inlining of the intersection function. Further the function-pointer adds another 16bytes to the ray-class instead of 4bytes for a enum/u_int.
I tested both methods and since neither had a obvious performance lead i decided to go with the second option.
// Ray Definition +=
// Additional 76 bytes (on single percision) per ray!
Vector3f id; // inverse direction
Float s_yx, s_xy, s_zy, s_yz, s_xz, s_zx, // slopes
c_yx, c_xy,c_zy, c_yz, c_xz, c_zx; // precomputation
bool (Bounds3<Float>::*pt2Member)(const Ray &r, Float *tMax, Float *tMin) const;Next we need to implement the actual intersection test. Since the original source code is no longer available we have to derive the correct comparisions for each ray-type. Below is the example for a PPP-ray.
template<typename T>
bool Bounds3<T>::PPP(const Ray &r) const {
// 1: test origin compared to box
if ((r.o.x > pMax.x) || (r.o.y > pMax.y) || (r.o.z > pMax.z)
// 2: slope tests
|| (r.s_xy * pMax.x - pMin.y + r.c_xy < 0)
|| (r.s_yx * pMax.y - pMin.x + r.c_yx < 0)
|| (r.s_zy * pMax.z - pMin.y + r.c_zy < 0)
|| (r.s_yz * pMax.y - pMin.z + r.c_yz < 0)
|| (r.s_xz * pMax.x - pMin.z + r.c_xz < 0)
|| (r.s_zx * pMax.z - pMin.x + r.c_zx < 0))
return false;
return true; // 3: no intersection depth
// 4: calc tMin
Float t = (pMin.x - r.d.x) * r.id.x;
Float t1 = (pMin.y - r.d.y) * r.id.y;
if (t1 > t)
t = t1;
float t2 = (pMin.z - r.d.z) * r.id.z;
if (t2 > t)
t = t2;
return (t < r.tMax);
}Results
Slope
Running only the intersection test without calculating tMin value returned fairly bad results as can be seen in the table below. The renderer uses the tMax value of the ray to store the closest intersection that has been found so far. This allows the original implementation to reject later AABB-intersections if their intersection-depth is greater than the previous one, e.g. if the tMax value that is stored in the ray is larger than the calculated intersection depth t the AABB can be rejected. This lower rejection rate results in fairly slow runtimes.
Slope + tMin
In order to increase the rejection rate I calculated the tMin value for each intersection as an extra rejection test. As can be seen the hit-rate improved as expected However it it still a lot slower than the original implementation.
Slope + Original
To further increase the rejection rate i added the original test after the intersection test. The hit rate is now pretty much equal to the original as expected however the advantage early reject of the slope test is outweighed by the added computation of slope test as well as the added data to the ray class which itself reduces cache-locality and thus hinders performance. Even the original test without any additional calculation suffers by up to 20$ performance decrease just through adding the extra 76 Bytes of data.
Original
So why is original so good? Unlike a naive implementation the original also has precomputed values for the costly operations e.g. inverted ray-direction as well as an indication weather the direction is positive or negative. This allows for reduced computations compared to a naive ray-slab intersection test. Also all computed values (tMin, TMax) are used to reject as many AABB as possible thus reducing the total amount of intersections that need to be made.
Test + Original
This was my last attempt to improve the original implementation. From the other experiments i knew that adding data to the ray-class will hinder performance drastically. So most of the slope test is unusable. However every slope test starts by evaluating the rays origin with respect to the AABB pMin/pMax value depending on weather the rays- direction is positive or not.
// Early rejection before original test
if (
(dirIsNeg[0] && ray.o.x < bounds.pMin.x) ||
((!dirIsNeg[0]) && ray.o.x > bounds.pMax.x) ||
(dirIsNeg[1] && ray.o.y < bounds.pMin.y) ||
((!dirIsNeg[1]) && ray.o.y > bounds.pMax.y) ||
(dirIsNeg[2] && ray.o.z < bounds.pMin.z) ||
((!dirIsNeg[2]) && ray.o.z > bounds.pMax.z)
)
return false;This does produce very similar results to original implementation. So it seems that the extra calculation cost and the benefit of early rejection of some rays are about equal.
Render-time
|X | Original | Test+Orig. | slope | Slope+Orig. | slope+tMin | — | — | — | — | — bathroom | 58.7s | 58.8s | 74.8s | 65.8s | 67.8s glass drag | 71.5s | 74.5s | 120.5s | 92.5s | 81.5s dual drag | 41.3s | 41.4s | 59.4s | 48.4s | 50.4s glass drag | 81.1s | 82.2s | 237.9s | 68.9s | 90.6s
Ray-triangle intersection
The following table represents the ray-rejection rate or rather how many of of the performed triangle tests were successful. (Higher is better)
| AABB-Test | Bathroom | dual-Dragon | glass-Dragon |
|---|---|---|---|
| Original | 20.89% | 28.98% | 25.94% |
| Test + Orig. | 21.99% | 28.78% | 27.13% |
| slope | 8.21% | 14.70% | 13.39% |
| slope + Orig. | 19.86% | 28.00% | 23.94% |
| slope + tMin | 11.24% | 18.66% | 19.45% |